Cálculo muestral para un estudio de prevalencia de coronavirus en el Ecuador
En un artículo anterior mencioné que era necesario hacer un estudio de prevalencia a través de pruebas aleatorias de coronavirus una vez que empiece a disminuir su demanda en las distintas provincias. Las pruebas aleatorias permiten obtener un mejor estimado del porcentaje de contagio (formalmente conocido como prevalencia) y, a su vez, corroborar si el número de casos positivos realmente está disminuyendo o no. Afortunadamente, la capacidad del gobierno de hacer pruebas ha aumentado y ellos mismos ya han empezado a realizar pruebas aleatorias a través de un muestreo probabilístico en cada cantón.
Utilizando métodos estadísticos, calculamos que en el escenario “menos conservador” el gobierno debería hacer al menos 1500 pruebas aleatorias por población de estudio (provincia o cantón), y en un escenario “más conservador” hasta 3000 pruebas. Solo a través de un estudio prevalencia, las autoridades gubernamentales pueden estimar el porcentaje real de casos de coronavirus en el Ecuador y basarse en estadísticas reales para la toma de decisiones. Desde el lunes 13 de abril se aplica un semáforo que indicará si puede o no flexibilizarse la cuarentena en ciertas provincias o cantones. De subestimarse el grado de contagio en cierto sector del país y flexibilizar el distanciamiento social, ponemos poner en riesgo la vida de quienes viven ahí y empeorar el grado de contagio.
Cuando mencioné que debería realizarse al menos 1500 pruebas por cantón en el escenario “menos conservador”, quise denotar que tal número tal vez no produzca una estimación óptima del porcentaje real de casos. Ciertamente, más pruebas generan una mejor estimación. Sin embargo, más allá de 3000 pruebas no logramos disminuir significativamente el margen de error y estaríamos generando un desperdicio. Te invitamos a leer la metodología en la siguiente sección y a reproducir los resultados utilizando el código al final del este artículo.
Metodología
En estadística, el tamaño de la muestra (\(n\)) depende esencialmente de tres variables: el nivel de confianza del parámetro (\(z\)), la precisión o margen de error (\(d\)) y la prevalencia esperada o porcentaje esperado de contagio (\(P\)) (Naing, Winn, and Rusli 2006). La fórmula es la siguiente:
Para entender las variables anteriores plantearemos un ejercicio hipotético. Imaginemos que deseáramos calcular el porcentaje de fumadores hombres en Ecuador y utilizáramos un nivel de confianza (\(z\)) del 95% y un margen de error (\(d\)) del 5%. Si al final del estudio halláramos que el 20% de los individuos en nuestra muestra son fumadores, un margen de error del 5% significaría que el porcentaje de fumadores de la población total estaría en un margen del 15% al 25% (20% ± 5%). Por otra parte, un nivel de confianza del 95% significaría que si repitiéramos este ejercicio infinitamente, en el 95% de los casos el porcentaje de fumadores caería dentro del intervalo del 15% y 25%.
Volviendo al cálculo de prevalencia de coronavirus, un detalle importante de la fórmula es que el margen de error (\(d\)) depende del porcentaje esperado de contagio (\(P\)), el cual es un valor que nosotros mismos asignamos basándonos en una hipótesis o conjetura. Por ejemplo, si asumimos para el cálculo muestral que el 2% de los habitantes de la provinicia del Guayas están contagiados (\(P = 2\%\)), necesitaremos usar una precisión del 1% (\(d = 2\%/2\)).
Si colocamos diferentes valores de \(P\) en la formula anteriormente descrita, obtendremos los siguientes tamaños de muestra:
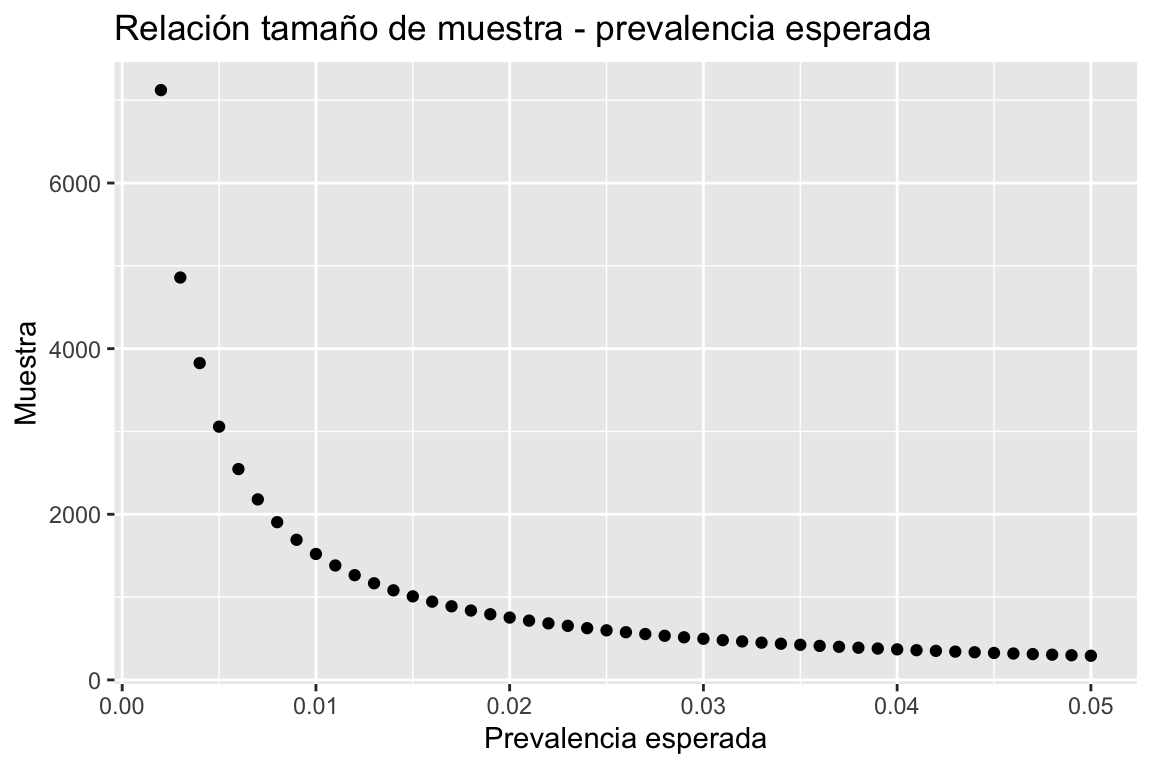
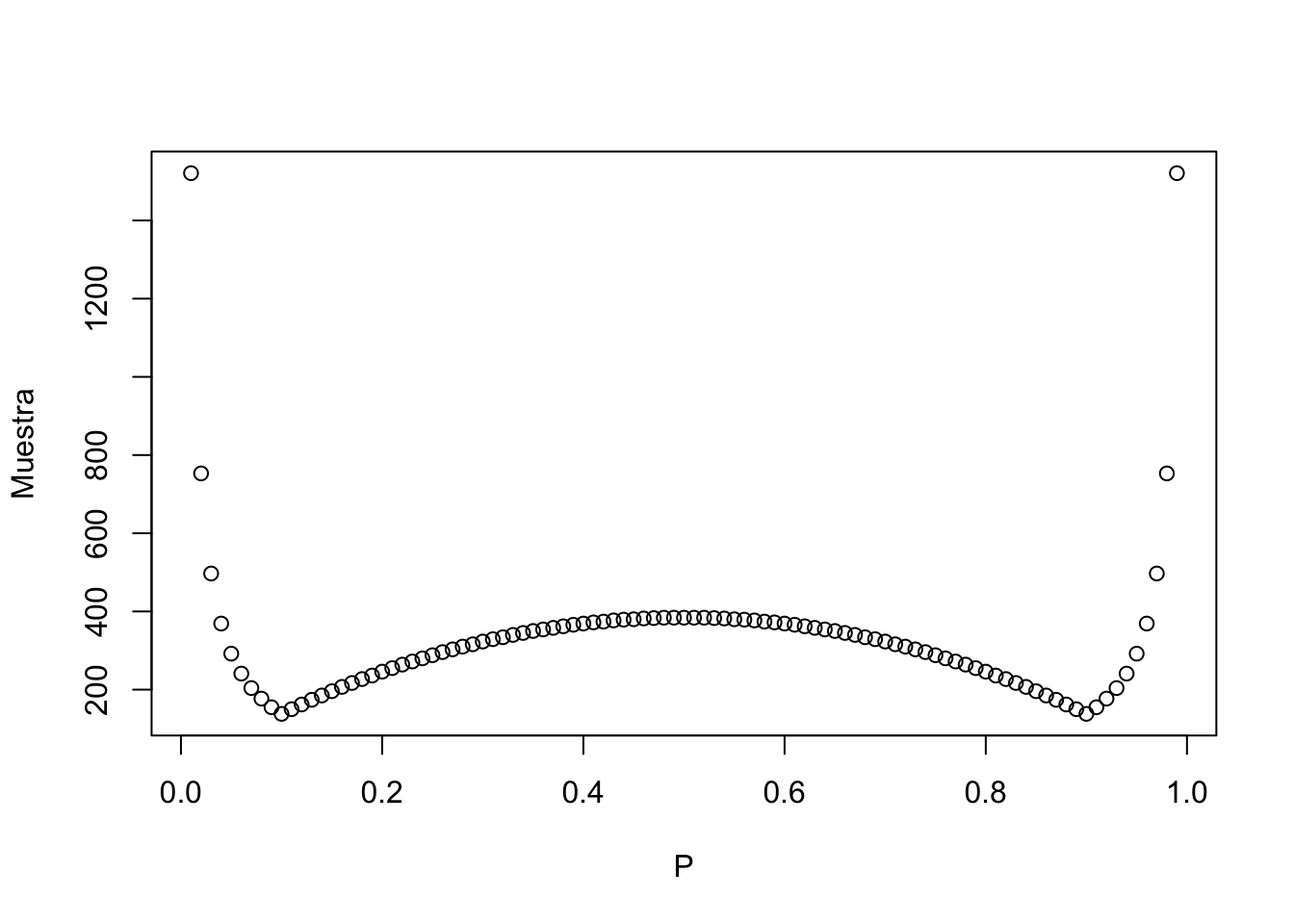
No debería sorprendernos que mientras menor sea el porcentaje de contagio esperado, mayor será el tamaño de la muestra. Esto se debe a que se hace cada vez más difícil encontrar casos positivos de coronavirus y estimar con mayor exactitud el porcentaje de contagio de la población se vuelve más un desafío. Asimismo, mientras mayor es el porcentaje esperado, menor es el tamaño de muestra necesario para inferir correctamente sobre la población total. Podemos notar también que la prevlencia esperada se acerca a cero, el tamño de la muestra empieza a tener al infinito. Incluso para valores muy pequeños de \(P\), una muestra muy grande se vuelve innecesaria y costosa. Mi recomendación (y esta es ya mi opinión) es apuntar a una \(P\) de entre 0.5% y 1% (es decir, una muestra por provincia de aproximadamente 1500 a 3000 individuos). Utilicemos una \(P\) de 1% para ver cómo se aplica la fórmula.
Cómo estimar la prevalencia esperada (\(P\))
En la práctica, para construir un mejor estimado de \(P\) se recomienda utilizar el resultado de estudios de prevalencia previamente hechos. Sin embargo, dado que este es un virus nuevo que aún estamos tratando de entender y que las estadísticas de contagio pueden estar muy segadas, no contamos con ningún estimado apropiado. Podríamos intentar dividir el número de casos confirmados de cada país para el total de sus habitantes y compararlo con el número de pruebas hechas, y así tratar de estimar un valor para \(P\).
Como podemos ver en el gráfico inferior, el porcentaje de contagio (confirmado) está altamente correlacionado al número de pruebas hechas. Esto tampoco debería sorprendernos ya que la manera más sencilla de no tener casos confirmados es no haciendo pruebas. Sin embargo, incluso tomando en cuenta este sesgo, podemos ver que los países que realizan mayor número de pruebas (a la derecha del eje horizontal) también poseen un bajo porcentaje de contagio (menor al 0.5%). Se ha dicho que mientras más pruebas se realizan, es más fácil rastrear a tiempo a los contagiados y distanciarlos en sus casas (como es el caso de Corea del Sur). Aunque estos países no sean el benchmark más indicado, podríamos apuntar en nuestro cálculo muestral a un \(P\) del 0.5%. Anteriormente realizamos un cálculo muestral considerando un \(P\) de 1.5% y obtuvimos un tamaño de muestral (por provincia o cantón) de 1,009. Ahora, si consideramos un \(P\) de 0.5%, y colocamos los valores en la fórmula, el tamaño de la muestra será de \(n = \frac{1.96^20.005(1-0.005)}{0.0025^2}\), lo cual equivale a 3,058.
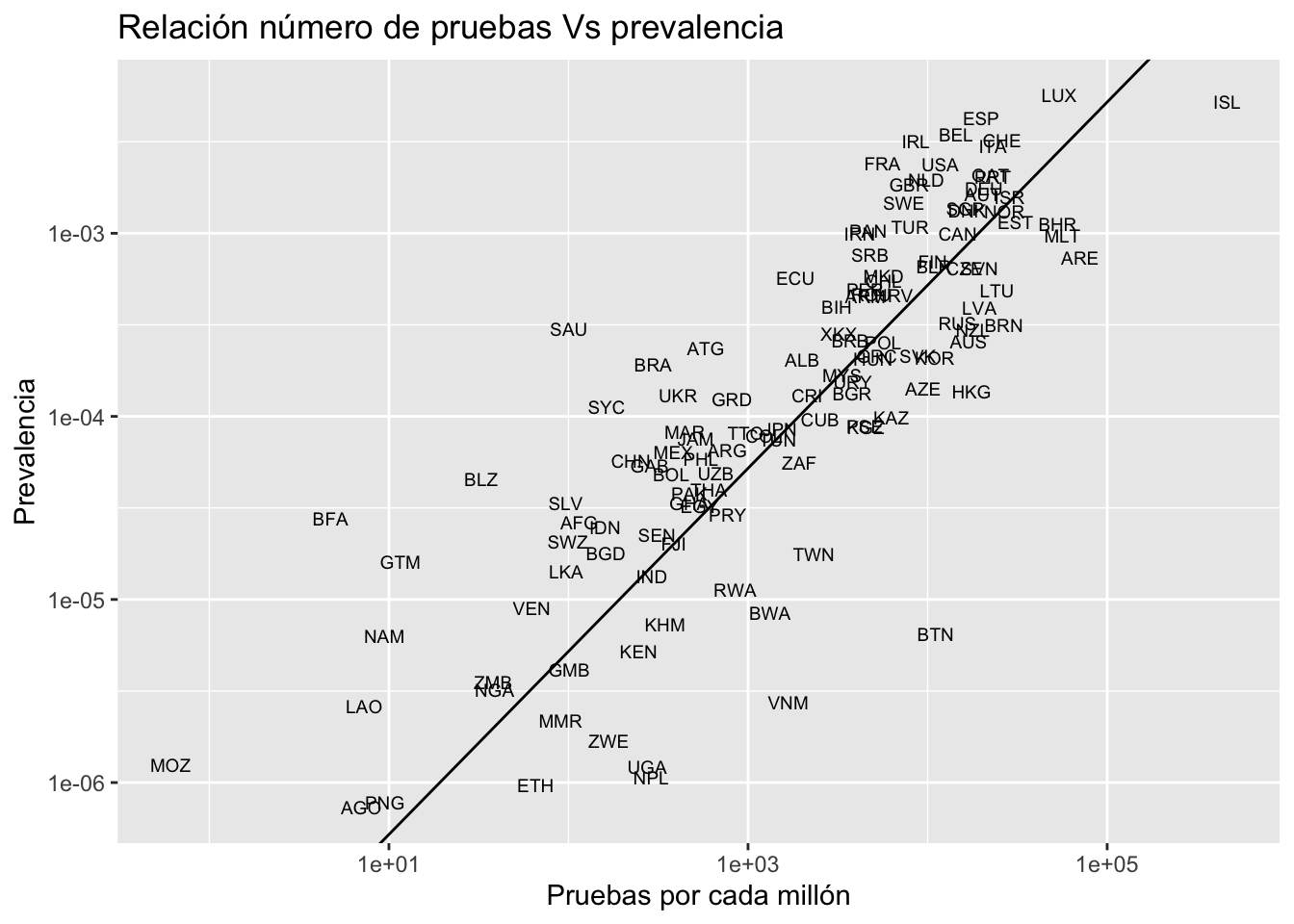 Fuente: Foundation for Innovative New Diagnostics
Fuente: Foundation for Innovative New Diagnostics
*Datos extraídos el 20 de abril de 2020
Cómo incluir el tamaño de la población en el cálculo de la muestra
La fórmula que usamos anteriormente \(n = \frac{z^2P(1-P)}{d^2}\) asume que el tamaño de la población (\(N\)), de la cual queremos estimar el porcentaje de contagio, es “grande” (o dicho jerga estadística “infinita”). Matemáticamente, esta fórmula asume que el tamaño de la muestra no debe ser superior al 5% del tamaño de la población o \(n/N < 5\%\). En caso de que la muestra sea mayor al 5% de la población, consideraremos a la población como “finita” y, por consiguiente, añadiremos al tamaño de la población (\(N\)) como variable en el modelo. La fórmula es la siguiente:
Digamos que deseamos realizar pruebas aleatorias en el cantón Baños de la provincia de Tungurahua. Este cantón tiene aproximadamente 25000 habitantes. Primero intentamos utilizar la primera fórmula que presentamos, la cual considera a la población como “infinita”. Considerando una prevalencia esperada \(P\) de 0.5%, obtenemos una muestra \(n = \frac{1.96^20.005(1-0.005)}{0.0025^2}\) equivalente a 3,058. Sin embargo, si dividimos este valor para el tamaño de la población, nos damos cuenta que la muestra es 12% de la población, mayor al umbral del 5% que habíamos establecido. En esta caso, nos tocaría utilizar la segunda fórmula \(n = \frac{N(z^2)P(1-P)}{d^2(N-1)+z^2P(1-P)}\), de la cual obtenemos una muestra de 2,725 individuos. El cálculo es el siguiente:
Bibligrafía
Naing, L, T Winn, and BN Rusli. 2006. “Practical Issues in Calculating the Sample Size for Prevalence Studies.” Archives of Orofacial Sciences 1: 9–14.
Apéndice
Si usas R y deseas reproducir los ejemplos en este artículo o realizar cualquier cálculo muestral, te invitamos a utilizar el código siguiente.
# ---------- Sample size formula ----------
sample_size <- function(z = 1.96, P = 0.5, d = 0.05, N) {
# We set a default of z = 1.96, expected prevalence or proportion (P) = 0.5,
# precision (d) = 0.05, N is an optional argument
d = ifelse(P > 0.9, (1-P)/2, # For common cases, we consider d = (1 -p)/2
ifelse(P < 0.1, P/2, d)) # For rare cases, we consider d = p/2
# Formula considering infinite population:
n = z^2 * P * (1 - P) / d^2
# We check if N is provided
if(missing(N)){
return(round(n))
} else {
# If n > N * 0.05, we consider a finite population
if(n > N * 0.05){
# Formula considering infinite population:
n = N * z^2 * P * (1 - P) /
( d^2 * (N - 1) + z^2 * P * (1 - P))
return(round(n))
} else {
return(round(n))
}
}
}
sample_size <- Vectorize(sample_size) # We vectorize the arguments of the function
# ---------- Simulating different sample sizes ----------
lambda <- seq(from = 0.99, to = 0.01, by = -0.01) # expected prevalences
# We calculate different sample sizes using the different prevalences
sample <- sapply(lambda, function(l){
sample <- sample_size(P = l)
return(sample)
})
df <- data.frame(P = lambda, Muestra = sample) # data frame to create the plot
plot(df)